http://www.escueladigital.com.uy/geometria/4_figplanas.htm
G E O M E T R Í A
SUMA DE FRACCIONES CON EJERCICIOS RESUELTOS

http://www.disfrutalasmatematicas.com/ejercicios/print.php?w=38771&ID=19309

http://www.disfrutalasmatematicas.com/ejercicios/fracciones.php

ADVERBIOS EJERCICIOS
http://www.apuntesdelengua.com/archivos/morfologia/adverbio/ejercicios02.pdf

EJERCICIOS IMPRIMIBLES
http://www.apuntesdelengua.com/blog/?page_id=1895

SOPA DE LETRAS DE ADVERBIOS
http://lenguayliteratura.org/mb/index.php?option=com_content&task=view&id=904&Itemid=1

ADVERBIOS Y PREPOSICIONES
http://roble.pntic.mec.es/msanto1/lengua/1adpreco.htm

EJERCICCIOS DE FRACCIONES RESUELTOS
http://www.matematica1.com/2012/04/ejercicios-resueltos-de-fracciones-y.html?spref=bl

http://www.ceibal.edu.uy/contenidos/areas_conocimiento/mat/comparaciondefracciones/recta_numrica.html

FRACCIONES EJERCICIOS RESUELTOS Y TEORÍA CURSO COMPLETO DE PRIMARIA , ESO Y SECUNDARIA VIDEOS+LIBRO PDF DESCARGA GRATIS

PÁGINAS PARA TRABAJAR MATEMÁTICAS

http://www.divulgamat.net/weborriak/RecursosInternet/RecInternet/Primaria/MatePrimaria1.asp
http://adigital.pntic.mec.es/cpr.utrillas/enlaces/matematicas.htm (enlaces por aspectos y/o niveles)
http://dewey.uab.es/pmarques/pdigital/webs/pri4mat.htm (enlaces para aspectos de 4º)
http://dewey.uab.es/pmarques/pdigital/webs/mates3prim.htm (todo 3º de primaria)

- Números:

http://roble.pntic.mec.es/~msanto1/ortografia/numrom.htm (números romanos)
http://www.escolar.com/matem/10decima.htm Explicación y ejercicio nº decimales
http://www.escolar.com/matem/11opdec1.htm Explicación , ejercicios de la suma, resta y multiplicación nº decimales
http://www.escolar.com/matem/12opdecii.htm División de nº decimales. Explicación y ejercicios http://www.escolar.com/matem/13nument.htm Explicación inicial y ejercicio nºs enteros
http://www.escolar.com/avanzado/matema065.htm Explicación inicial números enteros.
http://www.escolar.com/avanzado/matema066.htm Representación gráfica números enteros. Explicación.
http://www.escolar.com/avanzado/matema066.htm Relaciones de ordennúmeros enteros. Explicación.
http://www.escolar.com/avanzado/matema067.htm Plano cartesiano, suma y resta de nºs enteros

- Operaciones:

http://www.thebeehive.org/spanish/school/elementary/math.asp?subject=23 Juegos de suma, resta, multiplicación y división “on-line” y con comprobación de resultados 3º PRIMARIA
http://www.escolar.com/matem/06division.htm Explicación y ejercicios. Además explica muy gráficamente, con aplicaciones de Flash, la división exacta e inexacta y la división por números de 2 y 3 cifras.
http://www.escolar.com/matem/05multip.htm Explicación y ejercicios. Además explica muy gráficamente, con aplicaciones de Flash, las propiedades de la multiplicación: conmutativa, asociativa y distributiva; multiplicar por 10 y por 100; multiplicar por decenas; multiplicar por dos y tres cifras.

- Fracciones:

http://www.escolar.com/matem/08fracc.htm Explicación y ejercicios iniciación equivalentes mayores que unidad, menores…
http://www.escolar.com/matem/09opfrac.htm Suma, resta, producto de fracciones, fracción de un nº
http://www.escolar.com/matem/09b.htm División, simplificación, frac. inversas, potenciación frac.
http://clic.xtec.net/db/act_es.jsp?id=2060 Actividades clic 6º y ESO, suma, resta, producto…
http://clic.xtec.net/db/act_es.jsp?id=1340 Actividades clic para 6º. Operaciones con fracciones.
http://clic.xtec.net/db/act_es.jsp?id=1339 Actividades clic para 4º.Iniciación a los términos y representación de fracciones.
http://clic.xtec.net/db/act_es.jsp?id=1289 Actividades clic para 6º y ESO. Fracciones, múltiplos y divisores.

- Sistema Métrico Decimal:

http://www.educaguia.com/Servicios/software/software.htm Sist. Métr. Decimal actividades 4º
http://clic.xtec.net/db/act_es.jsp?id=1322 Mates 6º curso aritmética, medidas, geometría clic
http://www.escolar.com/matem/20medlong.htm Explicación gráfica e hipertextual sobre el Sistema Métrico Decimal (SMS), la unidad de medida, m. y los múltiplos y submúltiplos. También contiene ejercicios.
http://www.escolar.com/matem/22medvolu.htm Explicación y ejercicios sobre el volumen.
http://www.escolar.com/matem/21mesuperf.htm Explicación y ejercicios medidas de superficie.
http://sauce.cnice.mecd.es/~jdiego/problem/probquie/quiendijoprob1.htm Varias actividades que pretenden hacer pensar incluso a los más inteligentes, a través de ejercicios de razonamiento, problemas, números, cálculo y test matemáticos: operaciones matemáticas, potencias, ángulos, números enteros, fracciones, decimales, longitud, capacidad y masa, cuerpos geométricos, probabilidad, estadística, etc

- Conocimiento del Euro:

http://www.juntadeandalucia.es/averroes/recursos_informaticos/concurso02/accesit_4/index.htm Conocimiento del Euro, ejercicios diversos.
http://www.juntadeandalucia.es/averroes/recursos_informaticos/andared01/monedero/index.html Ejercicios de compra, venta, cambios con Euros.
http://clic.xtec.net/db/act_es.jsp?id=1313 Actividades clic iniciación al conocimiento de la moneda y billetes. Compras.
http://clic.xtec.net/db/act_es.jsp?id=1311 Actividades clic, familiarización con países y monedas Euro.
http://clic.xtec.net/db/act_es.jsp?id=1305 Actividades clic de relacionar, sumar, contar, problemas con moneda Euro.
http://clic.xtec.net/db/act_es.jsp?id=2059 Actividades clic. Cinco tipos de ejercicios para calcular con Euros.

-Medir el tiempo:

http://www.escolar.com/matem/19medtiem.htm Explicación gráfica e hipertextual sobre el sistema sexagesimal, las unidades de medida, de tiempo: hora y minuto y explicación sobre el día y el año. También contiene ejercicios.
http://www.educa.aragob.es/araclic/proyectos/proyectos.html ¿Qué hora es? Actividades clic repaso lectura horaria en reloj. Si se hace clic en la barra de herramientas, en primaria y luego en matemáticas aparece un nuevo paquete de estimación de precios para primer ciclo.
http://clic.xtec.net/db/act_es.jsp?id=1117 Tres paquetes de actividades para trabajar el nombre de las horas con relojes analógicos y digitales en catalán, español e inglés. Incluye imágenes y sonidos con el nombre de las horas.
http://clic.xtec.net/db/act_es.jsp?id=1213 Actividades clic de lectura de horas, cálculo de tiempo.2º ciclo de Primaria. Descargar la traducción en castellano.

- Problemas:

http://sauce.cnice.mecd.es/~jdiego/problem/probquie/quiendijoprob1.htm Varias actividades que pretenden hacer pensar incluso a los más inteligentes, a través de ejercicios de razonamiento, problemas, números, cálculo y test matemáticos: operaciones matemáticas, potencias, ángulos, números enteros, fracciones, decimales, longitud, capacidad y masa, cuerpos geométricos, probabilidad, estadística, etc

-Geometría:

http://www.educared.net/aprende/anavegar4/Mis%20Favoritos/Profesores/02borras/recursos.htm
http://www.kokone.com.mx/tareas/figuras/home.html
http://es.geocities.com/baldomeroab/t/EP_mate.htm
http://www.juntadeandalucia.es/averroes/recursos_informaticos/andared02/geometria1/index.html (buena para explicación de las figuras planas, por el profesor)
http://www.juntadeandalucia.es/averroes/recursos_informaticos/andared02/geometria3/inicio.html Ejercicio de coordenadas
http://www.walter-fendt.de/m11s/index.html Explicaciones del maestro de geometría, ESO
http://clic.xtec.net/db/act_es.jsp?id=1317 Actividades de geometría para primaria clic
http://clic.xtec.net/db/act_es.jsp?id=1368 Simetrías clic
http://clic.xtec.net/db/act_es.jsp?id=1303 Circunferencias y cuerpos geométricos clic
http://clic.xtec.net/db/act_es.jsp?id=1308 Geoclic 500 actividades 6º y ESO clic
http://www.educa.aragob.es/araclic/proyectos/proyectos.html Figuras planas 2º ciclo clic
http://clic.xtec.net/db/act_es.jsp?id=1322 Mates 6º curso aritmética, medidas, geometría clic
http://www.escolar.com/geometr/01punrec.htm Explicación y ejercicios sobre puntos, rectas, semirrectas y segmentos
http://www.escolar.com/geometr/02recang.htm Explicación y ejercicios sobre rectas paralelas y secantes, el ángulo, sus partes y tipos de ángulos.
http://www.escolar.com/geometr/03polig.htm Explicación y ejercicios sobre la línea poligonal abierta y cerrada (el polígono), sus elementos: los lados, los vértices y las diagonales. Figuras cóncavas y convexas. Polígonos regulares e irregulares.
http://www.escolar.com/geometr/05trian.htm Explicación y ejercicios sobre triángulos y su clasificación.
http://www.escolar.com/geometr/06cuadrila.htm Explicación y ejercicios sobre cuadriláteros y su clasificación.
http://www.escolar.com/geometr/13cuerpos.htm Explicación y ejercicios sobre los cuerpos geométricos y su clasificación: poliedros (regulares e irregulares i cuerpos rodantes.

-Rectas y ángulos:

http://www.escolar.com/geometr/01punrec.htm Puntos y rectas. Explicación y ejercicio
http://www.escolar.com/geometr/02recang.htm Paralelas y secantes, ángulos que se forman. Explicación y ejercicio
http://www.escolar.com/geometr/08angulos.htm Explicación y ejercicio de ángulo agudo, recto, obtuso, complementario, suplementario, adyacente, opuestos por el vértice…
http://www.escolar.com/avanzado/geometria007.htm Explicación de la clasificación de los ángulos

-Matemáticas y otras áreas:

-Teoría:

http://www.gesell.com.ar/vgol/locales/ong/iabgp/medida.htm (medida)
http://www.profes.net/rep_documentos/Monograf/AnPrimMatematicas.pdf
http://es.geocities.com/pizarraytiza/primaria.html (varias áreas)
http://es.geocities.com/pizarraytiza/ma3n.htm (relación de actividades)

-Herramientas:

-Entretenimientos matemáticos:

http://interactiva.matem.unam.mx/index_flash.html

-Actividades JClic de Matemáticas:

http://www.juntadeandalucia.es/averroes/real_mentesa/clic/index.htm

FRACCIONES

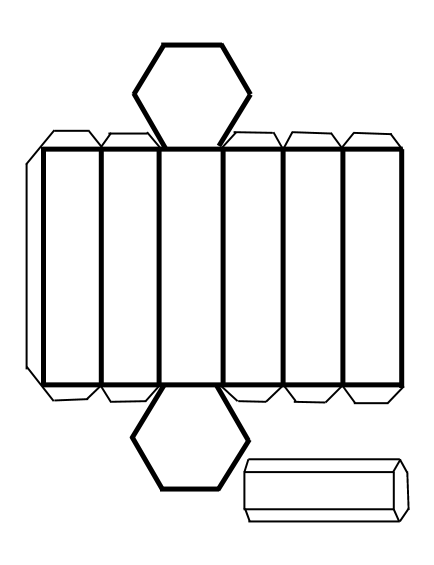
PRISMA HEXAGONAL

PRISMA PENTAGONAL

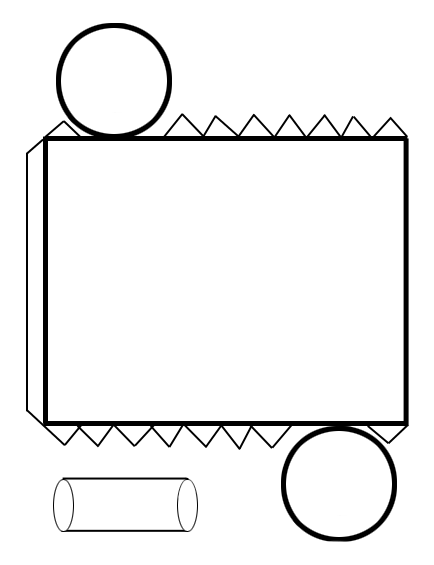
CILINDRO

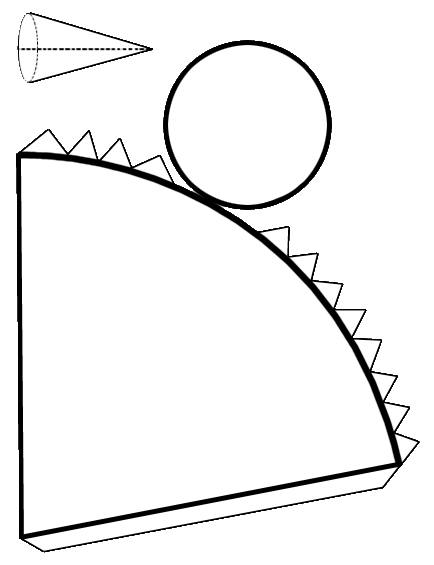
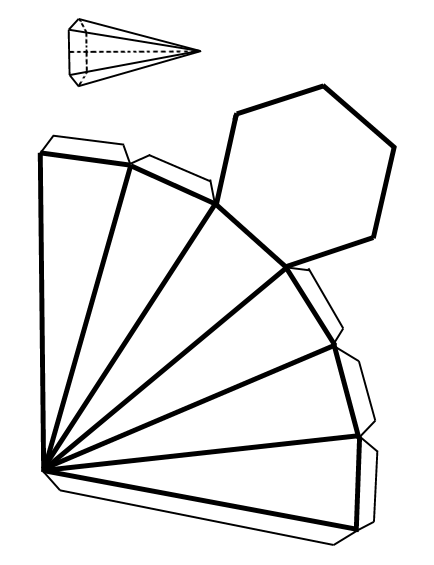
CONO

CUBO

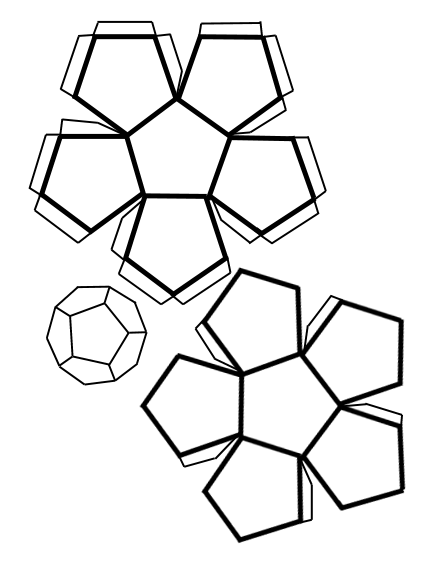
DODECAEDRO

ISOCAEDRO

OCTAEDRO

PIRAMIDE CUADRANGULAR

PIRAMIDE HEXAGONAL

PIRAMIDE OCTAGONAL

PIRAMIDE PENTAGONAL

PIRAMIDE TRIANGULAR

PRISMA RECTANGULAR

PRISMA TRIANGULAR

TETRAEDRO

ENLACES DE MATEMATICAS

Las figuras planas.

Utilicen este selector para ir a cada tema y volver al principio.
Las figuras planas | Líneas y puntos en los polígonos | Líneas y puntos en el círculo
Ángulos en los polígonos | Polígonos inscriptos y circunscriptos
Construcción de polígonos mediante el compás: Triángulo equilátero - Cuadrado
Exágono | Cálculo de la superficie de las figuras planas: Cuadrado - Rectángulo
Triángulo - Trapecio - Polígonos regulares - Círculo - Polígonos irregulares
--------------------------------------------------------------------------------
Las figuras planas.

El estudio de las figuras planas y sus propiedades geométricas, abarca a los polígonos en general — tanto regulares como irregulares — como así también al círculo, que puede ser considerado un caso especial de polígono.

Dicho estudio comprende:

Las relaciones referentes a las líneas, puntos y ángulos de los polígonos regulares;

Los métodos para el dibujo de los polígonos regulares;

Los métodos para el cálculo de la superficie de los polígonos regulares e irregulares.

Líneas y puntos en los polígonos.

En los polígonos regulares, se consideran las propiedades geométricas de las siguientes líneas y puntos:

El perímetro — que está formado por la continuidad, o la suma, de todos sus lados.

La diagonal — que es la línea que une dos ángulos no consecutivos.

El centro — que es el punto que se encuentra a una misma distancia de todos sus vértices.

El radio — que es la línea que une el centro con uno de sus vértices; por lo cual un polígono regular tiene tantos radios como ángulos.

El apotema — que es la línea perpendicular que une el centro con cualquiera de sus lados; por lo cual un polígono regular tiene tantos apotemas como lados.

Líneas y puntos en el círculo.

El círculo es la figura plana delimitada por la circunferencia; por lo que a los efectos geométricos equivale a un polígono regular con infinitos lados.

   En el círculo se consideran las propiedades geométricas de las siguientes líneas y puntos:

La circunferencia — que lo delimita, y que es el equivalente al perímetro.

El centro — es el punto del cual equidistan todos los puntos de la circunferencia.

El radio — es la medida de distancia entre el centro y la circunferencia, es el equivalente al radio de los polígonos regulares, y también al apotema.

El diámetro — que es la línea que pasando por el centro une dos puntos opuestos de la circunferencia, y por lo tanto mide el doble del radio, es el equivalente a la diagonal.

La secante — que es la línea que incluye dos puntos de la circunferencia, sin pasar por el centro. El tramo entre esos puntos, es la cuerda.

La tangente — que es la una línea recta que toca solamente un punto de la circunferencia.

El arco — que es el tramo de la circunferencia comprendido entre dos puntos distintos de la misma.

La flecha — que es la una línea perpendicular al punto medio de la secante, que lo une con la circunferencia.

El sector — que es la superficie comprendida entre dos radios y el arco que delimitan.

Los ángulos en los polígonos.

En los polígonos regulares se distinguen dos tipos de ángulos:

Los ángulos interiores — que son los que se forman en el vértice entre los lados.

Los ángulos centrales — que son los que se forman con vértice en el centro del polígono, y cuyos lados son los radios que unen ese centro a dos vértices consecutivos. Por lo tanto, un polígono regular tiene tantos ángulos centrales, todos iguales, como lados.

Por lo tanto, como la medida de la suma de todos los ángulos que pueden formarse alrededor de un punto, es de 360° la medida del ángulo central de un polígono regular es igual a 360 dividido por la cantidad de lados.

Ángulo central del triángulo equilátero: 360° ÷ 3 = 120°.

Ángulo central del cuadrado: 360° ÷ 4 = 90°.

Ángulo central del pentágono: 360° ÷ 5 = 72°.

Ángulo central del exágono: 360° ÷ 6 = 60°.

Ángulo central del octógono: 360° ÷ 8 = 45°.

Ángulo central del decágono: 360° ÷ 10 = 36°.

Polígonos inscriptos y circunscriptos.

Se dice que un polígono está inscripto en un círculo, cuando todos los vértices coinciden con puntos de su circunsferencia.
Se dice que un polígono está circunscripto en un círculo, cuando los puntos medios de todos sus lados coinciden con puntos de su circunsferenciConstrucción de polígonos mediante el compás.

Mediante la aplicación de los conceptos referentes a los ángulos de los polígonos, es posible servirse del instrumento de dibujo que es el compás, para construir graficamente diversos polígonos.

El compás es un instrumento básicamente aplicable en el trazado de circunferencias, que delimitan una figura plana que es el círculo; el cual puede ser considerado un tipo especial de polígono regular, en el cual todos sus lados están constituídos solamente por un punto, y cuya dimensión está determinada por la longitud del radio, que es equivalente a la abertura del compás.

El método a utilizar para construir polígonos mediante el uso del compás, se basa en determinar los vértices de los lados del polígono, estableciendo en qué puntos de la circunsferencia deben situarse para que el polígono resulte inscripto en ella.

Esa determinación se realiza a partir del conocimiento de los valores de los ángulos centrales del polígono que se desea construir.

Para trazar un triángulo equilátero inscripto en un círculo, manteniendo el radio (abertura del compás) empleado para trazar el círculo, se determina un punto de la circunferencia (preferiblemente en la vertical inferior de su centro), y centrando en ese punto se traza un arco con extremos en la circunsferencia.

Los puntos de intersección (A y B) determinan un lado del triángulo equilátero; por lo cual tomando la medida de ese segmento con el compás y trasladándola sobre la parte superior de la circunferencia, se determinará el vértice (C) de unión de los otros dos lados.

Para trazar un cuadrado inscripto en un círculo, se traza una recta que pasando por el centro llegue a la circunsferencia en sus extremos (diámetro AB).

Con una abertura del compás mayor a la empleada para trazar el círculo, centrando en los puntos extremos del diámetro, se marcan puntos en la circunferencia; lo que determinará dos nuevos puntos (C y D). Uniéndolos mediante una recta, resultará un nuevo diámetro perpendicular al anterior; cuyos puntos de contacto con la circunferencia serán los vértices del cuadrado inscripto.

Como el cuadrado inscripto queda en posición transversal, puede trazarse otro con los lados en posición horizontal y vertical, simplemente trazando las medianas del cuadrado anterior, para determinar los vértices A', B', C' y D', de un nuevo cuadrado inscripto en el mismo círculo.

Para trazar un exágono inscripto en un círculo, se fija un punto sobre la circunferencia, y con la misma abertura del compás, se marcan puntos haciendo centro primero en ese punto y luego sucesivamente en los nuevos puntos.

Ello determinará que se marquen sobre la circunferencia los seis puntos que corresponden a los vértices del exágono.

Cálculo de la superficie de las figuras planas.

La medida de la superficie de las figuras planas, se designa corrientemente en geometría con el nombre de área. Ella se expresa en unidades de medida de superficie, que se basan en la figura del cuadrado; por lo cual se llaman metros, decímetros o centímetros cuadrados.

El punto de partida para la determinación del método aritmético de cálculo de la medida de la superficie comprendida en las figuras geométricas planas, es el estudio del cuadrado.

Subdividiendo un cuadrado en varios cuadrados cuyo lado sea una parte del cuadrado original, resulta fácil apreciar que la cantidad de cuadrados menores — que pueden considerarse como unidad de medida — es igual a la multiplicación del número de cuadrados contenidos en dos de los lados del cuadrado originario: 5 × 5 = 25.

Conviniendo en denominar base al lado horizontal del cuadrado original, y altura el vertical; el procedimiento de cálculo de la superficie del cuadro puede expresarse en la fórmula:

SUPERFICIE DEL CUADRADO = BASE × ALTURA

En el caso del rectángulo, el mismo procedimiento permite establecer que el procedimiento de cálculo de su superficie es igual al del cuadrado: 5 × 8 = 40.

SUPERFICIE DEL RECTÁNGULO = BASE × ALTURA

La fórmula de cálculo del área del triángulo, es una derivación de las anteriores, atendiendo a que la diagonal de rectángulos lo divide en dos triángulos; por lo cual la superficie de todo triángulo es igual a la mitad de la del polígono que resultaría de duplicarlo tomando uno de sus lados como eje de simetría: 5 × 8 = 40 ÷ 2 = 20.

Si se observa un trapecio, se percibe que cada una de sus diagonales lo convierte en la suma de dos triángulos.

Por lo tanto, la superficie de un trapecio es la suma de las superficies de uno de los dos pares de triángulos que se forman al trazar una diagonal.

En el trapecio, se denomina base mayor al mayor de sus lados paralelos, y base menor al otro lado paralelo. De tal manera, la base mayor resulta ser la base de uno de los triángulos, y la base menor resulta ser la base del otro; en tanto que la altura del trapecio es la altura de ambos triángulos. Puede obtenerse la suma de ambas superficies en una única operación, sumando ambas bases, dividiendo el resultado entre 2, y multiplicando por la altura: 9 + 6 = 15 ÷ 2 = 7,5 × 5 = 37,5.

Propiedad fundamental de los polígonos regulares.

Observando las resultantes del estudio de las líneas de los polígonos regulares se detecta la siguiente propiedad fundamental:

En todos los polígonos regulares, el trazado de sus radios los divide en tantos triángulos como lados posean; cuyas alturas son iguales al apotema del polígono, y cuyas bases sumadas son iguales al perímetro del polígono.

En consecuencia, la superficie de un polígono regular será igual a la suma de las superficies de los triángulos que lo forman. Extendiendo la fórmula de cálculo de la superficie del triángulo, se deduce:

Superficie del círculo.

Considerando el círculo como un polígono regular cuyos lados son cada uno de los puntos que componen su circunferencia, ésta resulta ser su perímetro; y el radio es a la vez el apotema respecto de cada uno de esos puntos.

La circunferencia es una línea difícil de medir; pero puede calcularse a partir de la medida del radio, aplicando la propiedad fundamental del círculo.

La propiedad fundamental del círculo, consiste en que existe una relación permanente entre su radio y la medida de su circunferencia, que es un valor constante de 3,1416; el cual se designa con la letra griega PI.

En consecuencia, aplicando al círculo la regla general para el cálculo de la superficie de un polígono regular, se concluye:

Superficie de los polígonos irregulares.

Cualquier polígono irregular, puede descomponerse en triágulos, mediante el trazado de sus diagonales; o complementando éstas con perpendiculares desde un vértice a una diagonal.

Por lo tanto, conociendo la medida de las líneas que conformen las bases y alturas de esos triángulos, será posible calcular su superficie; y sumarla para obtener la superficie total del polígono irregular.

EN EL SIGUIENTE SUPER BLOG ENCUENTRAS VARIAS ACTIVIDADES
http://edhelper.com/Spanish/division.htm

Introducción a la división Conceptos de División (con gráficas de imágenes)
     Dividir entre grupos (números más pequeños)
     Dividir entre grupos (números más grandes)
     Divida en grupos (mezcla)
Conceptos de división con sobra gráficas
     Dividir entre grupos (números más pequeños)
     Dividir entre grupos (números más grandes)
     Divida en grupos (mezcla)
Datos de División (con gráficos)
     Escribe el dato de una división (con números más pequeños)
     Escribe el dato de una división (números más grandes)
     Escribe un dato de división (mezcla)
Multiplicación y división
     Llena el cociente
     Llene el número que falta
     Llene el número que falta
Suma y división
     Suma y división con 2
     Suma y división con 3
     Suma y división con 4
     Suma y división con 5
     Suma y división con 6
     Suma y división con 7
     Suma y división con 8
     Suma y división con 9
     Suma y división con 10
     Adición y división (mezcla)
Solución de problemas de división
     Resolviendo los problemas de división
Repaso mixto de división
     Repaso mixto de introducción a la división

División de Dígitos que faltan
     División con dígitos faltantes (2 dígitos divididos entre 1 dígito)
     División con dígitos faltantes (3 dígitos divididos entre 1 dígito)
     División con dígitos faltantes (4 dígitos divididos entre 1 dígito)
     División con dígitos faltantes (3 dígitos divididos entre 2 dígitos)
     División con dígitos faltantes (4 dígitos divididos entre 2 dígitos)
     División con dígitos faltantes (2 y 3 dígitos divididos entre 1 y 2 dígitos)
     División con dígitos faltantes (2 a 4 dígitos divididos entre 1 y 2 dígitos)

División de Rompecabezas de números !
^*Las siguientes hojas de trabajo son para suscriptores de edHelper.com.
Una suscripción a edHelper incluye el acceso a las áreas de suscripción de matemáticas, ortografía y vocabulario. Inscríbase para las materias de suscriptor.
     Introducción a División (gráficos)
     Cuántos 2 hay en 26 ...
     División (División horizontal entre 2 al 12)
     División (Llena el factor que falta)
     División (Números pequeños - Sin residuos)
     División (Números más grandes - Sin residuos)
     División (Residuos)
     División (Residuos 3 dígitos entre 2 al 12)
     División (Sin residuos 3 y 4 dígitos entre 2 al 12)
     División (Residuos 3 y 4 dígitos entre 2 al 12)
     División (mezcla de residuos y no residuos)
     División agrupada (incluye números -, + y 3+)
     Mezcla de Adición, Sustracción, División, y Multiplicación

Decimales de Rompecabezas de números !
     Multiplicación y División (sin restos)
     Multiplicación y División (más difícil - sin restos)
     Multiplicación y División (con restos)
     Mezcla de Adición, Sustracción, División, y Multiplicación

Rompecabezas de números cruzados del dinero de división de Rompecabezas de números !
     Multiplicación de Dinero (Rompecabezas de los Números)
     División de Dinero (Rompecabezas de los Números)
     Multiplicación y División de Dinero (Rompecabezas de los Números)
     Suma, Resta, Multiplicación y División de Dinero (Rompecabezas de los Números)

Fracciones de Rompecabezas de números !
     División
     División (Mezcla de Fracciones)
     Multiplicación y división
     Adición, Sustracción, Multiplicación, División

Números enteros de Rompecabezas de números !
     División
     Multiplicación y división
     Mixto
     Multiplicación y División (más...)

Secuencias de división de Rompecabezas de Secuencias !
Secuencias de división
Mezcla de Suma, Resta, División, Multiplicación

Multiplicación de fracciones de Hojas de Trabajos de Fracciones !
     División
     División (Mezcla de Fracciones)
     Multiplicación y división
     Adición, Sustracción, Multiplicación, División

Materiales del Suscriptor de EdHelper Solamente
^*Esta sección es para suscriptores de edHelper.com. Una suscripción a edHelper incluye el acceso a las áreas de suscripción de matemáticas, ortografía y vocabulario. Inscríbase para las materias de suscriptor.

El Tiempo: Televisión (Incluye División de Fracción)
Construya una hoja de práctica - 3 personas , 4 personas , 5 personas , 6 personas , 7 personas

Problemas verbales de multiplicación de la Sección de preparación para exámenes estandarizados de matemáticas

en esta pagina encuentras lo expuesto aquí

http://www.aaamatematicas.com/est.htm

Fracciones - Temas

Fracciones básicas

Sumar fracciones

Comparación de Fracciones

Comparar fracciones

Convertir fracciones

Dividir fracciones

Multiplicar fracciones

Reducir fracciones

Reglas de divisibilidad para ayudar a simplificar fracciones

Relaciones

Restar fracciones

Estimación - Temas

Redondear números

Redondear decimales

Estimació

EN ESTA OTRA PAGINA ENCUENTRAS ACTIVIDADES

http://www.disfrutalasmatematicas.com/numeros/index.html

¡Números ... !

Las habilidades con números valen diez veces más...

Cómo sumar, restar, multiplicar y dividir...
	Suma Resta Multiplicación División y División Larga

Cómo trabajar con Decimales...
1.23	Menú de Decimales

Cómo trabajar con Porcentajes...
	Menú de Porcentajes

Cómo trabajar con Fracciones...
	Menú de Fracciones

Álgebra, el siguiente paso después de los Números...
	Menú de Álgebra

Aquí hay más enlaces:

Contar
Contar Saltando

Reglas de Divisibilidad

División Larga
División Larga con Restos
División Larga con Decimales

Multiplicando Negativos
Juego con Números
Ordenando Decimales
Porcentaje
Proporción
Cuadrados y Raíces Cuadradas
Tablas de Multiplicar
Test de Tablas de Multiplicar

Más (ingles):

Base Conversion Method
Binary, Decimal and Hexadecimal Numbers
Binary to Decimal to Hexadecimal Converter
Binary Digits
Binary Number System
Hexadecimal Colors
Hexadecimal Multiplication Table
Hexadecimals

Avanzada:

Números transcendentes

Números algebraicos

Números complejos

Números primos y compuestos

http://www.sectormatematica.cl/

http://www.sectormatematica.cl/recreativa/cuento.htm

http://www.sectormatematica.cl/online/olimp1.htm

http://www.sectormatematica.cl/online/olimp7.htm

http://www.sectormatematica.cl/educbasica.htm

http://www.escolares.net/

http://miclase.wordpress.com/2007/06/18/aparato-digestivo-3/

Ejercicios de lectura y escritura

EJERCICIOS PARA TRABAJAR LOS ADVERBIOS

http://www.apuntesdelengua.com/blog/?page_id=1895

http://lenguayliteratura.org/mb/index.php?option=com_content&task=view&id=904&Itemid=1

ADVERBIOS
Indica los adverbios existentes en las siguientes oraciones:

.
Los chicos no han hecho los deberes esta tarde
Esos cajeros también están estropeados
La cabaña estaba más lejos de lo que pensábamos
Hoy lo haremos así, pero mañana quizás cambiemos
Se comporta amablemente, pero detrás hay algo raro
Sorprendentemente, el ejercicio les pareció demasiado fácil
Los dos coches estaban muy cerca
El favorito no es el corredor alemán
El bar estaba completamente vacío
No vengas ahora, ven después
Félix cumplió el encargo rápidamente
Nuestros vecinos volverán mañana
Me duele mucho esta muela
El profesor nos dio las notas ayer
María hablaba bastante
Allí encontramos a Luisa
Nunca supimos la verdad
Vivíamos muy cerca
No te vistas
Ellas sabían demasiado

http://www.sierradesanpedro.org/lenguaylit/adverbios/advI.htm

JERCICIOS PARA CONJUGAR VERBOS EN PRESENTE PRETERITO,

[PDF]
Ficha para practicar LA MORFOLOGÍA VERBAL (III)

http://www.apuntesdelengua.com/archivos/morfologia/verbo/VERBOS-FICHA03.pdf

20- Subrayar los verbos del siguiente fragmento que se encuentran en

modo subjuntivo e indicar persona y número de cada uno

“Yo soñé que soñaba. Y soñé que despertaba del segundo sueño,

del sueño soñado, y decía: “Ah, fue un sueño”, y creía estar despierto.

Quizá la vida sea eso, un sueño metido dentro de otro. Quizá la vida

sea el tercer sueño concéntrico del que uno despierta cuando muere”

21-Coloca en el espacio en blanco el verbo conjugado que falta. Al

final de la oración está indicado el infinitivo del verbo y el tiempo y el

modo que es necesario reponer

MATEMATICAS PARA 5° Y 6°, y otros contenido de naturales PARA MIS ALUMNOS, DIAGONALES,VERICES, FORMULAS ETC.

FRACCIONES EN EJERCICIOS CON ENUNCIADO O LITERALES